Here is last week’s puzzle as previously presented:
This past weekend, our family has had an amazing time up in a north Georgia cabin. One of the many activities we got to enjoy with the kids was researching, folding, and then flying paper airplanes.
From the topmost balcony on the cabin (three stories up!) both Max and Nora achieved great distances with their throws. This led to an interesting question: Could a paper airplane be thrown so far that it went around the world?
This week’s puzzle deals with airplanes circumnavigating the globe. Imagine an airplane that, by itself and fully fueled, could fly exactly half way around the world. This amazing plane can give and receive any amount of its fuel in mid-air instantly, can turn on a time, but can only take off and land at a single airport where it can also refuel.
Now imagine a fleet of these airplanes.
This week’s GeekDad Puzzle of the Week: Could a fleet of such airplanes, transferring fuel as appropriate, circumnavigate the globe? If not, why not? If so, how many planes would it take, and how could they accomplish such a feat?
Note that we want a repeatable process, so no planes can crash mid trip, and while the planes can’t glide they can land perfectly well using their last few atoms of fuel.
The biggest challenge in this puzzle was trying to come up with proper descriptions of the three key variables: time, the distance traveled, and the amount of fuel. As these can be set as arbitrary values within the constraints of the problem, let’s work with:
- The circumference of the earth is 360 units.
- It takes 1 unit of fuel to traverse 1 unit of earth.
- Any and all planes can hold 180 units of fuel.
- Traversing the earth takes 6 hours, i.e., 360 minutes.
- It takes 1 minute to traverse 1 unit of earth.
Under this set of time / fuel / distance values, we can see that it would only take a flight of 3 Planes (total) to circumnavigate the globe.
But just how do they do it?
All three Planes take off fully fueled, heading in the same direction. At 1/8 of the way around (45m), Plane C gives 1/3 of its fuel (45 units) to each of the other two Planes. Planes A and B at this point are now full refueled. Plane C then heads home to land just as its fuel is exhausted.
Plane C then starts a 3-hour period of rest and relaxation, perhaps going to catch a movie or have an adult beverage. In the case that there are multiple similar circumnavigatory flight efforts going underway, with proper scheduling, the same Plane C could support three efforts; instead of 3 Planes per lead Plane flight, it would only take 5 Planes to support two big arc flights (instead of 6) and only 7 Planes for three (instead of 9.)
In any case, after another 45m, as Plane C is landing (above), Plane B gives Plane A 1/3 of its fuel (45 units.) This completely refuels Plane A, and leaves Plane B 90 units of fuel. Both Planes A and B are 90 units of distance from the home base. Plane B turns around and heads home, landing just as its fuel is exhausted.
For the next 180m, Plane A flies solo, with no support. This moves it from 90 units away from base to 270 units / -90 units away from base (coming from the other direction.) While Plane C is not flying, Plane B is quite busy; after landing on the last few atoms of its fuel (above), it immediately refuels and takes off in the opposite direction to meet Plane A once again. The landing and take-off occur at time 180m from initial takeoff, and Plane B starts with a full tank of 180 units of fuel. At this point in time, Plane A is at the midpoint of its solo flight (location of 180 away from base in either direction), and has 90 units of fuel remaining.
Planes A and B reunite at distance 270 units / -90 units, where Plane A is just starting to run completely out of fuel, and Plane B has just 90 units remaining. They split the 90 units from Plane B evenly (45 units each,) and both head back towards the base to complete the circuit for Plane A. The time is now 270m after initial departure, and Plane A has been moving continuously in the same direction the entire time. Of course, with Planes A and B being 90 units away with only 45 units of fuel each, they need to engage Plane C.
At this point, Plane C’s movie is over, and it leaves base heading toward Planes A and B with a full 180 units of fuel. After 45m, at a distance of 45 units from base, it encounters Planes A and B — who are both just about to run out of fuel completely. Plane C has 135 units of fuel remaining, and it gives Planes A and B 45 units of fuel each. This leaves 45 units of fuel for Plane C, and all three Planes are able to (just barely) fly the 45 units of distance back to base.
I have a full spreadsheet of Time / Position / Fuel for each of the three Planes for anyone who would like to see it.
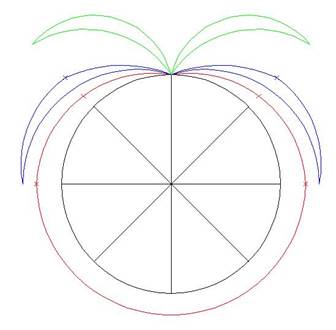
Many thanks to everyone that posited a solution, and a hearty congratulations to Ben Hoogenboom, winner of the random drawing from among the set of correct (or at least reasonably correct) responses submitted. Not only did Ben provide a correct solution but he also provided both a nice “radar plot” style diagram for each Plane (shown below) as well as a set of detail activities for Plane C including “playing XBox,” “enjoying a long bath,” and “reading up on Reddit.”
Here is the diagram of each Plane’s journey (Plane A in Red, Plane B in Blue and Plane C in Green.)
A $50 gift certificate from ThinkGeek will be making its way to Ben very soon — hopefully not being delivered by one of these Planes.
Thank you for reading GeekDad and shopping at ThinkGeek and happy puzzling!




Haha I didn’t think of re-using Plane C so I called it four planes, but of course there were only 3 in the air at once in mine too.