This past week’s counting conundrum, as previously published:
This week’s GeekDad Puzzle of the Week is based around the number “1” (one) and the number of times the number appears in the set of counting numbers. In the set of numbers from 1 to ten, the digit “1” appears twice: once on the “1”, and then again on the “10.” If we keep a running total, we can see that there are 12 “1s” present counting from 1 to 20.
1 1 11 4 2 1 12 5 3 1 13 6 4 1 14 7 5 1 15 8 6 1 16 9 7 1 17 10 8 1 18 11 9 1 19 12 10 2 20 12 For the most part, it seems like the running count of observed 1s is far lower than the number up to which we have counted at that point; at 100, we have only seen 21 ones, and at 1000 only 301.
Is this true for all counting numbers under 10 million? That is, are there runs of observable counts that equal or exceed the number up to which we have counted at that point? If so, what are they? If not, why is it not possible?
It turns out that not only is it possible, but for numbers under 10,000,000 (ten million), there are three areas where the running count of 1s exceeds the running count of natural numbers.
Plotting the running count of 1s observed against the running count, we get:
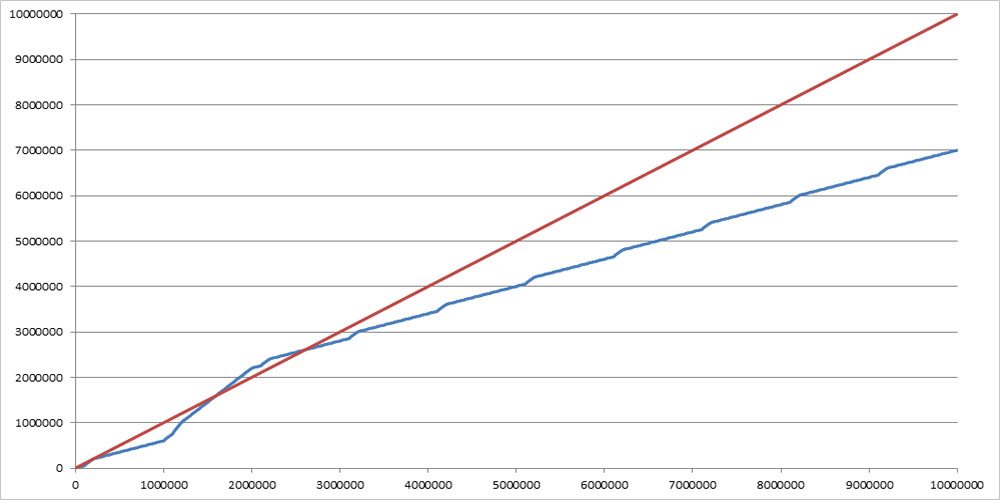
Here, we can see that there is a range where the running count of 1s observed (blue) exceeds the count (1:1 line, red) in the 1.5 million to the 2.5 million range. Additionally, we can see that the lines might mix in the 200,000 neck of the woods.
Zooming in around 200,000, we can see that the running count of 1s (blue) does meet and exceed the count (red), as shown here:

Finally, we have the trivial case for n=1, i.e., there is one “1” counting from 1…1.
The entire set of counting numbers under ten million where the running count of 1s meets or exceeds the running count goes is as follows:
| Start | End | run Length |
|---|---|---|
| 1 | 1 | 1 |
| 199,981 | 200,001 | 21 |
| 1,599,981 | 2,600,001 | 1,000,021 |
There were 25 values for which the two values were equal. Looking at OEIS Sequence A014778, these are 25 out of the 84 total (with the next two values being 13,199,998 and 35,000,000.)
The average amount the running count of 1s exceeded the running count was around 118,885, with the largest overage clocking in at 200,001. It hits this values through two ranges of counting numbers: from 1,999,991 to 1,999,999 and from 2,199,991 to 2,199,999.
Congratulations to D. Schneider for finding the intervals and values above, and for being drawn at random from the correct (or reasonably well-reasoned) responses submitted. A $50 Gift Certificate from our friends at ThinkGeek is on its way!
Thanks to everyone that entered a response to this week’s GeekDad Puzzle of the Week, and for reading GeekDad.
Happy puzzling!





