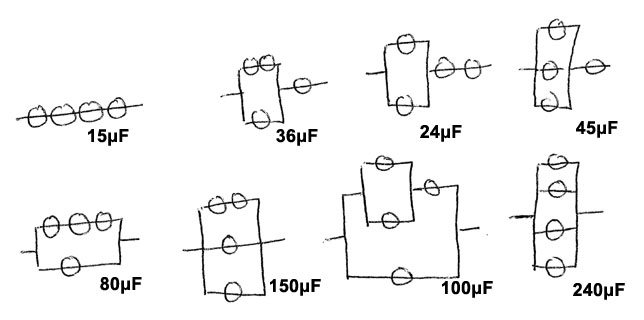
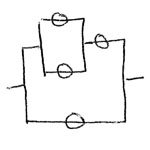
Last week’s engineering-based puzzle as posted:
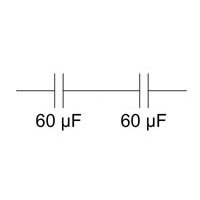
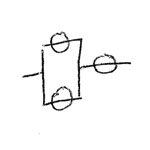
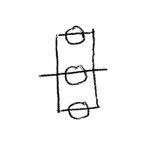
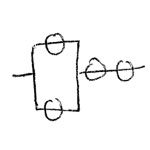
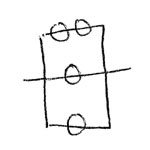
Looking back to my Physics coursework, one of the most interesting (and challenging) aspects was calculating the overall capacitance of a set of capacitors. As you may recall, capacitors in parallel sum the capacitance of each element; in series, they are the inverse of the sum of the inverses of each element.Put graphically:
Capacitors in Parallel: Capacitors in Series: 60 µF + 60 µF = 120 µF 1/(1/60 µF + 1/60 µF) = 30 µF There’s only one way to “wire in” a single 60 µF capacitor, and three different ways to wire in up to two 60 µF capacitors – one by itself, two in series, and two in parallel.
This week’s GeekDad Puzzle of the Week is to determine how many different capacitance values can be created by wiring together up to 10 identical 60 µF capacitors. Note that not all 10 need to be used for each circuit, and that subsets can be used in parallel and in series to each other.
This week’s puzzle was straightforward, as long as you didn’t get too wrapped up in the math. If you think of each incrementally larger circuit as a circuit one capacitor smaller plus the new capacitor either in series or parallel, you will be on the right track.
For example:
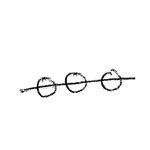 in series with
in series with 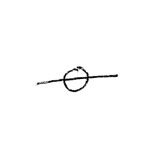 =
= 
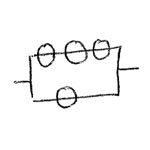
and
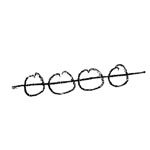
 in parallel with
in parallel with  =
= 
For the first capacitor counts, we get:
1 @ 60 µF Capacitor:
|
|
2 @ 60 µF Capacitor:
|
|
|
3 @ 60 µF Capacitor:
|
|
|
|
|
4 @ 60 µF Capacitor:
|
|
|
|
|
|
|
|
|
|
|
|
|
Of course, with the last two examples, you can see that not each value of overall capacitance is unique, as
 ,
, 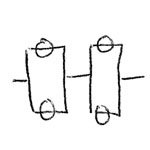 , and
, and  all provide 60 µF of capacitance.
all provide 60 µF of capacitance.
This provides us:
| n | Number of distinct wiring diagrams using exactly n @ 60 µF capacitors | Number of distinct capacitance values using exactly n @ 60 µF capacitors | Number of distinct capacitance values using up to n @ 60 µF capacitors |
| 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 3 |
| 1 | 4 | 4 | 7 |
| 1 | 10 | 9 | 15 |
| 1 | 24 | 22 | 35 |
| 1 | 66 | 53 | 77 |
| 1 | 180 | 131 | 179 |
| 1 | 522 | 337 | 429 |
| 1 | 1532 | 869 | 1039 |
| 1 | 4264 | 2213 | 2525 |
There are 2,525 different capacitance values can be created by wiring together up to 10 identical 60 µF capacitors.
Congratulations to David Pelletier, this week’s winner of the $50 ThinkGeek Gift Certificate. Thanks to everyone that submitted an entry.